Camera Pose Estimation via Projective Newton Optimization on the Manifold
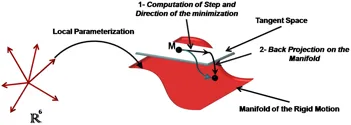
Projective Newton-type algorithm on the manifold: A local parameterization maps the variables from R6 to the manifold. The minimization is then performed in two steps: The optimization direction and step size are computed on the tangent space to the manifold. The calculated values are then projected back on the manifold to update the motion.
Abstract:
Determining the pose of a moving camera is an important task in computer vision. In this paper, we derive a projective Newton algorithm on the manifold to refine the pose estimate of a camera. The main idea is to benefit from the fact that the 3D rigid motion is described by the Special Euclidean group which is a Riemannian manifold. The latter is equipped with a tangent space defined by the corresponding Lie algebra. This enables us to compute the optimization direction, i.e. gradient and Hessian, at each iteration of the projective Newton scheme on the tangent space of the manifold. Then, the motion is updated by projecting back the variables on the manifold itself. We also derive another version of the algorithm that employs a homeomorphic parameterization to the Special Euclidean group. We test the algorithm on several simulated and real image data sets. Compared to the standard Newton minimization scheme, we are now able to obtain the full numerical formula of the Hessian with 60% decrease in the computational complexity. Compared to Levenberg-Marquardt, the results obtained are more accurate while having a rather similar complexity.
Reference:
M. Sarkis & K. Diepold, “Camera Pose Estimation via Projective Newton Optimization on the Manifold”, IEEE Trans. Image Processing, (Accepted for Publication)
Paper: Download
Code: Download
Please consider referring this paper if you use any of the developed algorithms in this paper in your publications. For enquiries about the algorithm & bug reports please contact the author Michel Sarkis at: misarkis(at)gmail.com.