Globally-optimal solutions for unit-norm constrained computer vision problems

Participants:
- Supervisor: Prof. Dr.-Ing. habil. Alois Christian Knoll and Prof. Dr. Guang Chen
- PhD student. Yinlong Liu
- MSc. Judith Treffler
Background and Motivation
Nowadays, computer vision algorithms are increasingly applied in many safety-critical applications. Usually, the failure or malfunction are determined to be unacceptable in safety-critical applications. For example, if we cannot provide safety guarantee for self-driving system that is a typical safety-critical application, it may lead to some serious failures, even the death of people. Therefore, it is highly needed that the computer vision algorithm should return the extremely reliable solutions in safety-critical applications.
However, in real applications, noise and outliers are unavoidable and it is well-known that even one outlier input may bias the results significantly. In practice, the de facto outlier-robust algorithm in computer vision is RANSAC(RANdom SAmple Consensus). However, RANSAC is a non-deterministic algorithm, which means it cannot return the provably optimal solution with guarantee. Besides, to suppress outliers, robust loss functions(e.g., Cauchy loss) are usually applied. However, the robust loss functions are usually non-convex and thereby the objective functions are usually non-convex. Unfortunately, it is not easy to optimize a non-convex optimization problem, because it contains many local optimums and many gradient-based algorithms have the risks of being trapped in local optimums. Therefore, to meet the safety demand in safety-critical applications, globally-optimal solutions, which can provide theoretical guarantees that the reported optimal solution is indeed the best one, should be explored in presence of noise and outliers.
Theory
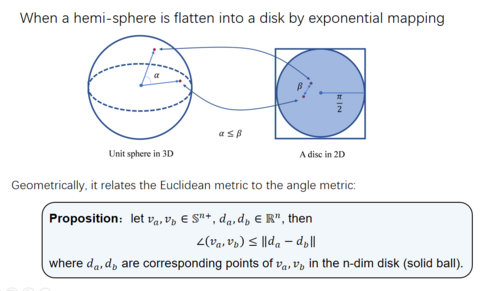
Specifically, the globally optimal solutions are provided by the branch-and-bound algorithm, which is a deterministic global optimization algorithm. Moreover, to obtain global optimums for unit-norm constrained optimization problems, we explore the geometry of the unit-norm constraint and introduce a general inequality for n-sphere.
Applications
Based on the introduced general inequality and the branch-and-bound algorithm, three different unit-norm constrained computer vision tasks are studied to seek globally optimal solutions. Specifically,
a. Globally optimal solution for estimating vertical direction from the Atlanta world. This work is about globally estimating the unique vertical direction in Atlanta world. Compared with the state-of-the-art methods, it has two advantages: (1) avoiding the curse of dimensionality in Atlanta world; (2) avoiding manual adjustment of the number of horizontal directions. Methodologically, the contributions are mainly as follows: (1) A novel global searching method for estimating vertical direction is proposed. It is different from conventional rotation search. Since the domain of the vertical directions is inherently in the unit sphere, the proposed searching method is more efficient in vertical direction estimation. (2) Three novel different bounds for branch-and-bound algorithm are derived. To the best of our knowledge, it is the first to propose such bounds in the unit sphere to the structural world frame estimation problem.
[1] Yinlong Liu, Guang Chen, and Alois Knoll. "Globally Optimal Vertical Direction Estimation in Atlanta World." IEEE Transactions on Pattern Analysis and Machine Intelligence (2020). DOI: 10.1109/TPAMI.2020.3027047
paper: https://ieeexplore.ieee.org/abstract/document/9207842
b. Globally optimal solution for camera orientation estimation from 2D-3D line feature correspondences. This work is concerned with the problem of estimating camera orientation from a set of 2D/3D line correspondences, which is a major part of the Perspective-n-Line (PnL) problem. The RANSAC algorithm is the de facto standard for solving outlier-contaminated PnL problems. However, RANSAC cannot produce a reasonable result with a provable guarantee. Therefore, a PnL algorithm that could obtain a certifiably optimal solution from outlier-contaminated data is highly needed. We take a big step towards this goal. Specifically, we first decouple camera orientation and position, then a globally optimal camera orientation estimation algorithm is investigated.
[2] Yinlong Liu, Guang Chen and Alois Knoll, "Globally Optimal Camera Orientation Estimation from Line Correspondences by BnB algorithm," in IEEE Robotics and Automation Letters, vol. 6, no. 1, pp. 215-222, Jan. 2021, doi: 10.1109/LRA.2020.3037843.
paper: https://ieeexplore.ieee.org/document/9258393
c. Globally optimal solution for camera relative pose estimation with known vertical direction. Recently, there has been a surge of interest in using prior gravity direction to solve traditional robot vision problems, However, most of them focus on solving outlier-free problems. To obtain a robust solution from outlier-contaminated inputs, we propose a globally optimal algorithm for relative pose estimation with known gravity direction. The proposed method employs the branch-and-bound algorithm to solve a consensus maximization problem, and thus it is able to obtain the global solution with a provable guarantee. The proposed algorithm has important potential to be used in some safety-demand applications.
[3] Yinlong Liu, Guang Chen, Rongqi Gu and Alois Knoll, "Globally Optimal Consensus Maximization for Relative Pose Estimation with Known Gravity Direction," in IEEE Robotics and Automation Letters, doi: 10.1109/LRA.2021.3087080.