DFG-Priority Programme Control Theory of Digitally Networked Dynamical Systems (SPP 1305)
Control theory develops methods for the modelling, the analysis and the control of dynamical systems by using the principle of feedback. One of its characteristical tasks is to measure a specific variable, compare it with a nominal value and change the performance of the system so that the variable follows the prescribed value. Hitherto the required data exchange for the implementation of feedback control could only be managed in a wired way.
Modern means of communication lays the foundations to connect different elements of the system like sensors, actuators or even whole subsystems to a digital network. By the implementation of wireless connections over a wide area new control laws can be realised that would have been much more complex to realise in a wired network, if even possible. Furthermore, measured variables and control variables can now be transmitted to the controller from nearly every position of a technological plant.
Such control structures cannot be handled with traditional methods because of two reasons. On the one hand, the event-driven mode of operation of digital networked systems violates the presumption that data is processed and transmitted with a constant sample rate. On the other hand, the structure of the network is changing since the data link adjusts itself to the needs and the technical constraints.
The goal of the interdisciplinary Priority Programme SPP 1305 is to develop a control theory for the modelling, analysis and design of future digitally networked dynamical systems.
Two-layer distributed optimization and control approach for large-scale interconnected systems
ITR participates in the subproject "Two-layer distributed optimization and control approach for large-scale interconnected systems" in collaboration with the Chair of Mathematical Optimization (TUM).
The design of optimization and control algorithms for complex dynamical systems has become a vibrant part of research due to its wide applicability and impact with applications ranging from smart power grids, water distribution, and traffic systems to large arrays of Micro-Electro-Mechanical Systems (MEMS), formation of vehicles, and sensor-actuator networks.
The optimization and control of such large-scale systems is computationally expensive and thus calls for distributed algorithms. Novel approaches applying digital communication networks for controlling large-scale systems are known under the notion of distributed control.They are based either on distributed optimization, and therefore are advantageous with respect to performance but may not quickly react to dynamic changes, or on distributed feedback control mechanisms that guarantee stability even in the presence of fast dynamic changes.
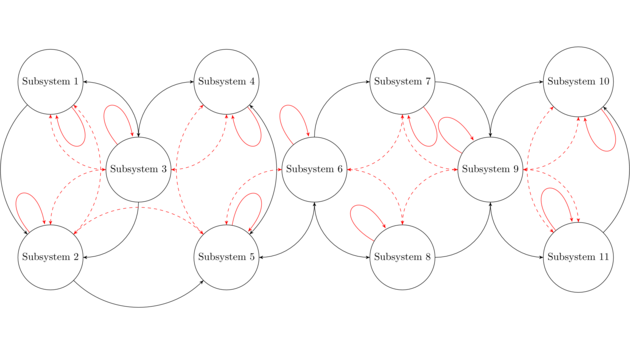
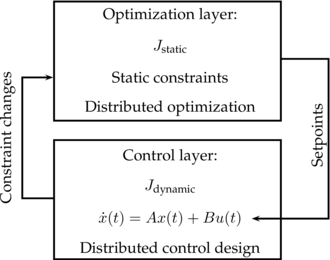
So far, no approach exists that addresses both main challenges of optimal performance and quickly changing dynamics in large-scale systems. The innovative idea of this project is to develop a two-layer distributed control architecture for large-scale systems combining distributed optimization with distributed feedback control approaches. Thereby the advantages of optimization in terms of performance benefits are combined with the advantages of feedback control in terms of stability guarantees with fast dynamic changes for distributed systems. We consider heterogeneous large-scale interconnected systems where the dynamics of each locally controlled subsystem is modelled as linear timeinvariant system. The optimization-based part is responsible for decision making on a higher level of abstraction and a slower time-scale generating setpoints for the clusters. Feedback control mechanisms, on the other hand, track the setpoint given by the optimization layer as well as stabilize the system even in the presence of fast dynamic changes.
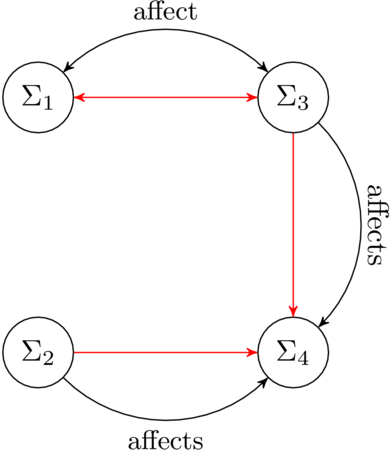
More concretely, the developed control design approaches aim at a design using limited (local) model knowledge for each subsystem without any global model information. The design approach uses an iterative distributed gradient descent method. The necessary information exchange of the three principle phases of each iteration are visualized below and it is obvious that only neighborhood information is required.