Foundations of Signal Processing
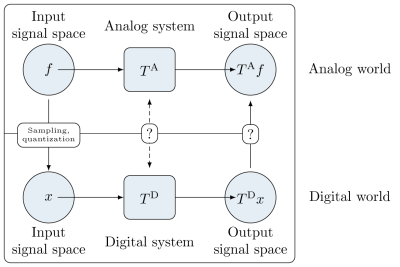
A main driving force in the development of our current information society is digital signal processing, the central idea of which is to implement analog systems using digital methods. The advances in digital signal processing are stimulated by the enormous performance increase of integrated circuits. Moore's law says that the complexity of integrated circuits doubles approximately every two years. Classically, the necessary theory has been developed for linear systems and signals in
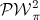
, i.e., for bandlimited signals that are square integrable. However, for several applications, a rigorous theory for other classes of function spaces is needed. We analyze signal and system representations for the Paley-Wiener space
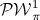
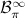
of bounded bandlimited signals. We also consider non-equidistant sampling patterns and oversampling. In practical applications quantization is an integral part of the analog to digital conversion. A deterministic analysis of the quantization process is difficult because of the nonlinear nature of the quantization operator, but it reveals properties of the quantization process which cannot be analyzed with the common additive noise description of the quantization error.